PDF:

---

Context: It is hypothesized that a fifth force of nature can be observed as interplanetary interactions. Here, we look at potential evidence that Earth acts on Mars according to the expression when Earth-Mars distance is less than Earth-Sun distance; C is some positive constant; is Mars’ latitude from Earth; and T and M are Earth’s sidereal rotation period and mass, respectively. A full description can be found here: Mathematical Model Used to Predict Interplanetary Phenomena

---

During 1875 – 2023, there were 70 periods when Earth-Mars distance was less than Earth-Sun distance with each period averaging 6.7 months in duration. Of these, 46 included observations of dust storms on Mars [Figure1, Ref1]. Months that included global dust storms coincided with these periods 100% of the time; Encircling 38%; Regional 79%; Local 65%; Dust cloud 50% [Table1].

A total of 211 out of 1788 months included dust storm observations (11.8%). In other words, we should expect dust storm observations in 35.34 out of the 70 periods if there were no relationship between Martian dust storms and Earth’s position [Appendix 1]. Therefore, the data suggests that there are 15.2% () more periods coinciding with dust storms than we should expect.

Based on an expected frequency of 35.34 periods with dust storms, we performed a binomial test to assess the significance of this observed difference. The resulting p-value was p=0.007224146, indicating that the observed frequency significantly exceeds the expected value at the 1% significance level.

The next period will be Nov 4 2024 – Mar 16 2025 (4.4 months), which includes the upcoming opposition. We calculated a 43.2% chance of observing a dust storm based on this data [Appendix 2]. If there were no relationship between Martian dust storms and Earth’s position, then this figure should be 42.5% [Appendix 3]. So for this amount of time, there is no practical difference.

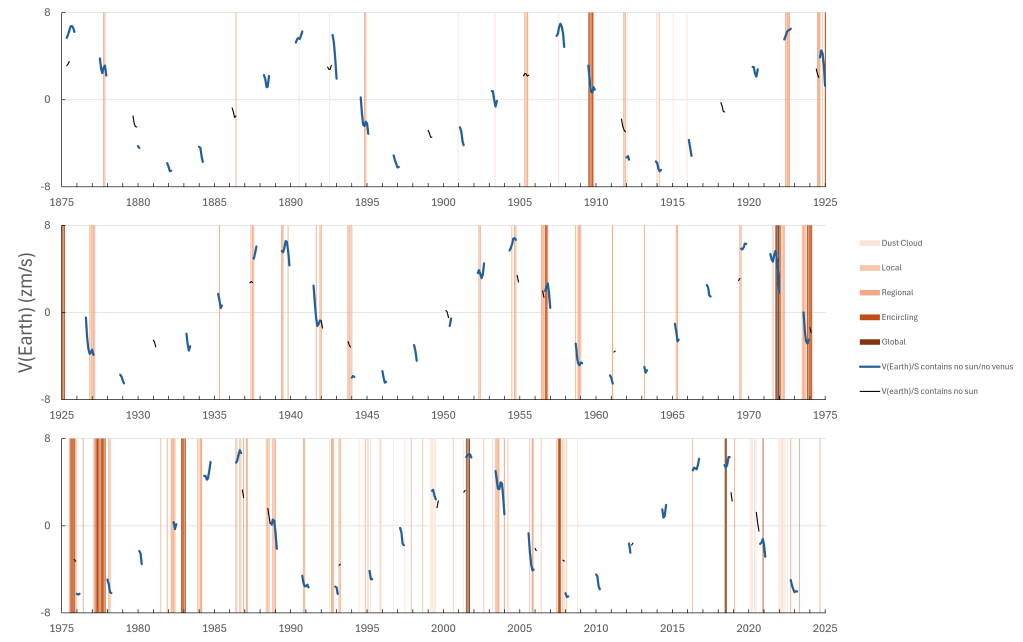
Figure 1

Table 1

During V(Earth) periods, the near side of Mars to Earth should experience a slightly stronger force than the far side. Therefore, we might expect a loose correlation between the latitudinal positions of the onset of dust storms and Earth’s latitude from Mars. Figure 2 shows latitudinal positions of dust storms during V(Earth) periods and Earth’s latitude from Mars. There is a suggestion of a loose correlation, which could benefit from regressional analysis.

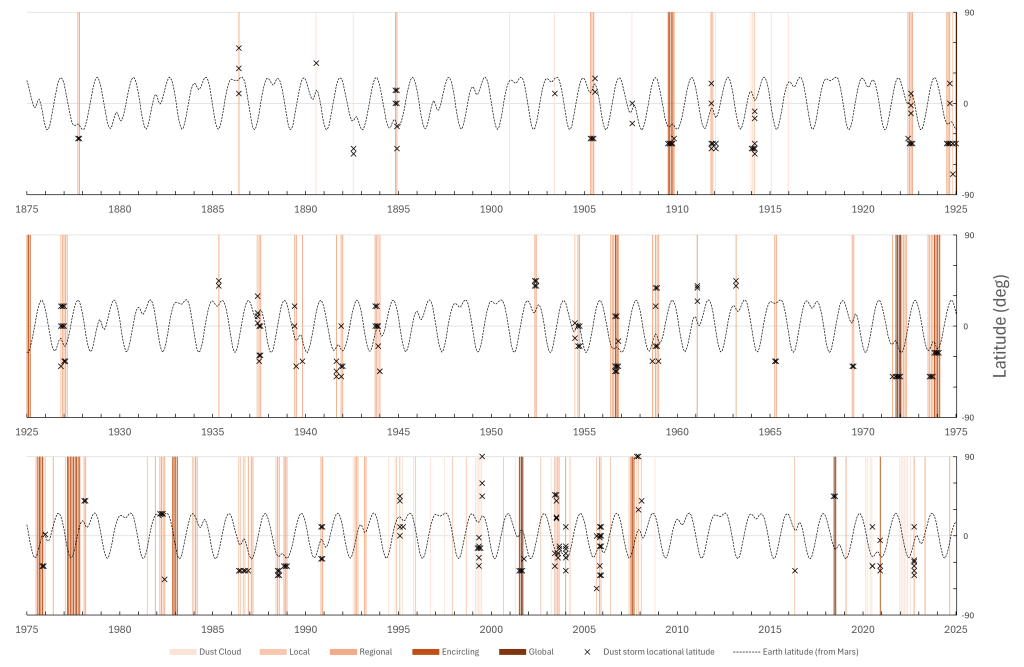
Figure 2

References

1. Dust storm information from Jeff Beish’s “A Revised List of Dust Storms on Mars (Revised August 04, 2024).”

Appendix 1

Expected number of periods out of the 70 during 1875-2023 where at least one dust storm was observed:

1. Determine the Probability of No Dust Storm in a Given Period

If we know the probability of observing a dust storm in a single month, we can calculate the probability of not seeing a dust storm in that month as:

2. Calculate Probability of No Dust Storms in an n-Month Period

For each n-month period, if we assume that the probability of a dust storm in each month is independent, the probability of no dust storms occurring across the entire period is:

3. Calculate Probability of at Least One Dust Storm in a Period

The probability of observing at least one dust storm in a period is simply the complement of the probability of no dust storms:

4. Calculate Expected Number of Periods with Dust Storm Observations

Finally, to get the expected number of periods (out of the 70) with at least one dust storm, we sum these probabilities over the total number of periods:

Given , we used these steps to find that 35.34 out of 70 periods should have at least one dust storm observation.

Appendix 2

The probability that at least one dust storm will be observed during a 4.4 month period based on the given data is

Appendix 3

The probability that at least one dust storm will be observed during a 4.4 month period given there is no relationship with Earth’s orbit is